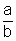Se define polinomio a todas aquellas funciones que tienen una estructura formada por términos, coeficientes y variables, además de exponentes que indicarán el grado del polinomio.
Las variables son letras: x, y, z, a, b, c...
Los coeficientes son números enteros o fraccionarios, positivos o negativos que acompañan a las variables multiplicandolas.
Los términos son expresiones separadas por signos de suma y resta.
Los exponentes son números siempre positivos y que son potencia de la variable.
El grado del polinomio es el exponente mayor de la variable, se utiliza para identificar cuando se tiene términos semejantes.
Los términos semejantes tienen la misma variable y el mismo grado, entre ellos se pueden hacer operaciones de suma y resta.
lunes, 22 de febrero de 2016
Operaciones con polinomios
Adición de polinomios
La suma de polinomios es una operación en la que partiendo de dos polinomios P(x) y Q(x), obtenemos un tercero R(x), que es la suma de los dos anteriores, R(x) tiene por coeficiente de cada monomio el de la suma de los coeficientes de los monomios de P(x) y Q(x) del mismo grado.
Para sumar expresiones polinomicas de dos o mas números se suman los términos, que son semejantes entre si, lo cual equivale a sumar unidades con unidades, decena con decenas, centenas con centenas, etc.
La suma de polinomios es una operación en la que partiendo de dos polinomios P(x) y Q(x), obtenemos un tercero R(x), que es la suma de los dos anteriores, R(x) tiene por coeficiente de cada monomio el de la suma de los coeficientes de los monomios de P(x) y Q(x) del mismo grado.
Para sumar expresiones polinomicas de dos o mas números se suman los términos, que son semejantes entre si, lo cual equivale a sumar unidades con unidades, decena con decenas, centenas con centenas, etc.
- Ejemplo:
Sustracción de polinomios
Para restar dos polinomios se suma al minuendo el opuesto del sutraendo, es decir, se cambia el signo a todos los términos del segundo polinomio (sustraendo) y se suman los resultados.Para restar el polinomio Q(x) del polinomio P(x) se debe sumar a P(x) el polinomio opuesto de Q(x).
P(x) - Q(x) = P(x) + [ - Q(x)].
P(x) - Q(x) = P(x) + [ - Q(x)].
- Ejemplo:
P(x) − Q(x) = (2x3 + 5x - 3) − (2x3 - 3x2 + 4x)
P(x) − Q(x) = 2x3 + 5x - 3 − 2x3 + 3x2 − 4x
P(x) − Q(x) = 2x3 − 2x3 + 3x2 + 5x− 4x - 3
P(x) − Q(x) = 3x2 + x - 3
Multiplicación de polinomios
La multiplicación de polinomios es una operación algebraica que tiene por objeto hallar una cantidad llamada producto dadas dos cantidades llamadas multiplicando y multiplicador, de modo que el producto sea con respecto del multiplicando en signo y valor absoluto lo que el multiplicador es respecto a la unidad positiva. Tanto el multiplicando como el multiplicador reciben el nombre de factores del producto.
La multiplicación de polinomios cumple la propiedad distributiva. Es decir, que dados tres polinomios cualesquiera  se cumplirá que
se cumplirá que  . Esta ley acostumbra a enunciarse diciendo que los factores se pueden agrupar de cualquier manera.
. Esta ley acostumbra a enunciarse diciendo que los factores se pueden agrupar de cualquier manera.
Asimismo, el producto de polinomios también cumplía la propiedad conmutativa. Es decir, que dados los polinomios cualesquiera  , se cumplirá que
, se cumplirá que  . Esta ley acostumbra a enunciarse diciendo que el orden de los factores no altera el producto.
. Esta ley acostumbra a enunciarse diciendo que el orden de los factores no altera el producto.
Multiplicación de polinomios
Para multiplicar un polinomio por otro se multiplican todos los términos del multiplicando por cada uno de los términos del multiplicador, teniendo en cuenta la regla de los signos, y a continuación se efectúa la suma algebraica de todos los productos parciales así obtenidos.
- Ejemplo:
División de polinomios
La división algebraica es la operación que consiste en hallar uno de los factores de un producto, que recibe el nombre de cociente dado el otro factor, llamado divisor, y el producto de ambos factores llamado dividendo.
De la definición anterior se deduce que el dividendo coincide con el producto del divisor por el cociente. Así por ejemplo, si dividimos  , se cumplirá que
, se cumplirá que  .
.
Para dividir dos polinomios se procede de la manera siguiente:
1) Se ordena el dividendo y el divisor con respecto a una misma letra.
2) Se divide el primer término del dividendo entre el primer término del divisor, obteniéndose así el primer término del cociente
3) Se multiplica el primer término del cociente por todo el divisor y el producto así obtenido se resta del dividendo, para lo cual se le cambia de signo y se escribe cada término de su semejante. En el caso de que algún término de este producto no tenga ningún término semejante en el dividendo, es escribe dicho término en el lugar que le corresponda de acuerdo con la ordenación del dividendo y del divisor.
4) Se divide el primer término del resto entre el primer término del divisor, obteniéndose de este modo el segundo término del cociente.
5) El segundo término del cociente se multiplica por todo el divisor y el producto así obtenido se resta del dividendo, cambiándole todos los signos.
6) Se divide el primer término del segundo resto entre el primer término del divisor y se repiten las operaciones anteriores hasta obtener cero como resto.
- Ejemplo
Dividir: 
productos notables
Llamamos productos notables a ciertas expresiones algebraicas
que resultan de una multiplicación que es preciso factorizarlas de una manera
inmediata
Tipos de productos notables:
Producto notable
|
Expresión algebraica
|
Nombre
|
|
(a + b)2
|
=
|
a2 + 2ab + b2
|
Binomio al cuadrado
|
(a + b)3
|
=
|
a3 + 3a2b + 3ab2 +
b3
|
Binomio al cubo
|
a2 - b2
|
=
|
(a + b) (a - b)
|
Diferencia de cuadrados
|
a3 - b3
|
=
|
(a - b) (a2 + b2 +
ab)
|
Diferencia de cubos
|
a3 + b3
|
=
|
(a + b) (a2 + b2 - ab)
|
Suma de cubos
|
a4 - b4
|
=
|
(a + b) (a - b) (a2 +
b2)
|
Diferencia cuarta
|
(a + b + c)2
|
=
|
a2 + b2 + c2 +
2ab + 2ac + 2bc
|
Trinomio al cuadrado
|
Por ejemplo:
1. (2 + x)² = 2² + 2(2) (x) + x²
Diferencia de cuadrados
Por ejemplo:
1. x6 - 4 = (x3 + 2).(x3 - 2)
2. x2 - 9 = (x + 3).(x - 3)
Suma de cubos:
Ejemplo:
8x3 + 27 = (2x + 3) (4x2 - 6x + 9)
Diferencia cuarta
Ejemplo
1.
b4 - 81 = (b - 3).(b3 + 3b2 + 9b + 27)
Trinomio cuadrado
fracciones algebraicas
Fracciones algebraicas
Una fracción algebraica es una expresión fraccionaria en la
que el numerador y denominador son
polinomios.
por ejemplo:
Las fracciones algebraicas tienen un comportamiento similar a las fracciones numéricas.
El valor de una fracción no se altera si se multiplican o dividen el
numerador y denominador por una misma cantidad. Esta cantidad debe ser distinta
de cero.
Operaciones con fracciones algebraicas
Simplificar fracciones algebraicas
La simplificación de
fracciones algebraicas es igual al de las fracciones ordinarias: dividiendo el numerador y el denominador
por factores comunes. Entonces, la clave está en el factor común. Para
simplificar al máximo habrá que factorizar los polinomios numerador y
denominador.
Por ejemplo, simplificar:
Otro ejemplo, simplificar la fracción
Primero, factorizamos los polinomios del numerador y del denominador,
para quedar
Suma y resta de fracciones algebraicas
Para sumar y restar procederemos de forma similar a como lo
hacemos con fracciones de números enteros, reduciendo primero a común denominador.
Igual como ocurre con las fracciones de números enteros, la
suma y resta de fracciones algebraicas puede ser con fracciones de igual
denominador o de distinto denominador.
Suma y resta de fracciones
algebraicas con igual denominador
Veamos el siguiente ejemplo de suma y resta:
Ahora sacamos los paréntesis teniendo
cuidado de cambiar el signo interior cuando delante del paréntesis hay un signo
menos (−), y nos queda
Suma y resta
de fracciones algebraicas con distinto denominador
Veamos el siguiente ejemplo:
Entonces, que debemos
hacer: encontrar el m.c.m. de
los denominadores, que llamaremos mínimo común denominador (m.c.d.). (No confundir con M.C.D, Máximo Común Divisor) Multiplicamos
los factores y queda a • a • b • b • 5 • 3 = a2 • b2 • 15 que es lo mismo que 15a2b2 y
es el mínimo común denominador (m.c.d.) de las tres fracciones involucradas.
Conocido el m.c.d. operamos con fracciones con denominador
común:
Previamente, dividimos el denominador común (15a2b2) por
cada uno de los denominadores individuales, para conocer la cifra o valor que
se multiplica por cada uno de los numeradores, y lo hacemos así:
Producto (multiplicación) de fracciones
algebraicas
Para multiplicar fracciones algebraicas procederemos igual
como lo hacemos con fracciones, multiplicando los numeradores y los denominadores, aunque antes de multiplicar debemos simplificar, si se puede.
Veamos qué significa esto:
Multiplicar
Anotamos la multiplicación de los numeradores y de los
denominadores:
Simplificamos antes de efectuar el producto:
Ahora, podemos multiplicar los factores finales:
Cociente o división de fracciones
algebraicas
Para dividir fracciones algebraicas procederemos igual como
lo hacemos con fracciones, haciendo el producto cruzado de numeradores y denominadores,
aunque antes de multiplicar debemos simplificar, si se puede.
Veamos, ahora qué significa esto:
Veamos ahora ejemplos de división
(cociente) de fracciones algebraicas
Dividir
Anotamos haciendo el producto cruzado:
Simplificamos y finalmente multiplicamos:
Suscribirse a:
Comentarios (Atom)